F+闭包怎么求
- 第一步:设最终将成为闭包的属性集是Y,把Y初始化为X;
- 第二步:检查F中的每一个函数依赖
A→B,如果属性集A中所有属性均在Y中,而B中有的属性不在Y中,则将其加入到Y中; - 第三步:重复第二步,直到没有属性可以添加到属性集Y中为止。 最后得到的Y就是X+
X是题目会给出的,求谁(即X)的闭包;Y是最后所求得的闭包
设关系
R(A,B,C,D,E,G)有函数依赖集F={AB→C,BC→AD,D→E,CG→B},求AB的闭包
X =
{A、B}{A、B}+ = Y ={A、B、C、D、E}
由上可知,F逻辑蕴涵AB->D (因为D被{A、B}+包含)
关系模式的候选码怎么求
候选码:能唯一 完全函数依赖确定元组 的属性(或属性集合);候选码的闭包是全集U,没有冗杂
对应R< U、F>(U是属性集,F是函数依赖集)
- 如果有属性不在F中出现,那么它必须包含在候选码中
- 如果有属性在所有函数依赖中一直存在于左边,则它必包含在候选码中;同理只在右边出现过的属性一定不属于候选码
- 如果有属性或属性组能唯一标识元组,则它就是候选码
先用前两条,都不满足就凭借最后一条一个一个找
有时候选码不止一个,都细分一下
范式判断
- 候选码K:若K(属性或属性集合)可以完全函数依赖确定全部属性U,则K就是候选码
- 主属性:候选码的子集
- 1NF:【最基本的】 关系模式R的所有属性 域都是原子的(不可分的)
- 2NF:不存在非主属性对候选码部分函数依赖(也就是说非主属性完全函数依赖于候选码)
- 3NF:不存在非主属性对候选码传递依赖(第三范式又可描述为:表中不存在可以确定其他非主属性的非主属性)
BCNF:只要属性或属性组A能够决定任何一个属性B,则A的子集中必须有候选键(F的左侧包含超码)
范式之间是包含关系,1NF>2NF>3NF>BCNF(这里>表示包含)
分解成(无损连接的)BCNF范式
对于R<U、F>
- 初始化
result={R} - 找到R中的一个模式S不属于BCNF,且F+中存在一个
X->Y(Y不包含于X),X也不是S的候选码,则S就能分解为{S1、S2}。S1=XY,S2=(S-A)X,用{S1、S2}代替result中的{S} - 继续执行上面这步直到result中所有关系模式都是BCNF
例:关系模式
R<U,F>,其中U={C,T,H,R,S,G},F={CS→G,C→T,TH→R,HR→C,HS→R},将其分解成BCNF并保持无损连接
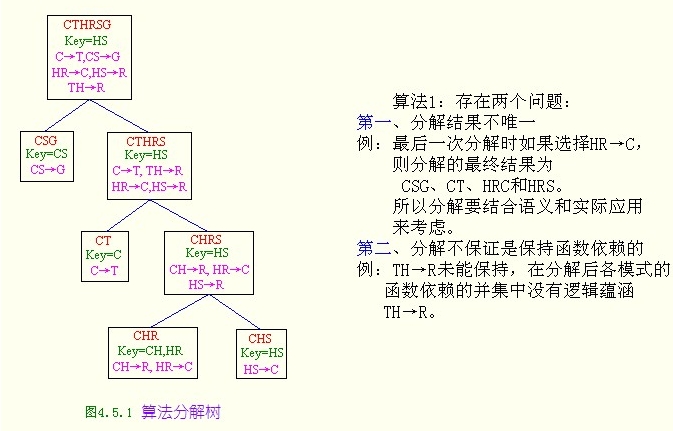
例:关系模式
R<U,F>,其中:U={A,B,C,D,E},F={A→C,C→D,B→C,DE→C,CE→A},将其分解成BCNF并保持无损连接。
result={ {A、C}、{B、D}、{A、B、E} }

